حتماً به خاطر دارید که بعد از کنکور ۱۴۰۰، چه هجمههایی بر سازمان سنجش بخاطر سوالات ریاضی وارد شد. این هجمهها در هر سه رشتهی ریاضی، تجربی و انسانی بر سازمان سنجش وجود داشت و دلیل آن غیراستاندارد بودن سوالات درس ریاضی بود. غیراستاندارد بودن سوالات از جهات زیر بود:
- وجود سوالات غلط
- وجود سوالات دشوار، بیش از حد معمول
- وجود سوالاتی با محاسبات سنگین و طولانی که در زمان کوتاه جلسهی کنکور، پاسخگویی به آنها میسر نبود.
- وجود سوالاتی خارج از مباحث کتاب درسی
- عدم رعایت بودجهبندی درست
با وجود انتقادهای درستی که به سازمان سنجش وارد شد، انتظار میرفت که سوالات درس ریاضی کنکور ۱۴۰۱ منطقیتر و متعادلتر باشد؛ که این اتفاق هم دقیقاً افتاد و سوالاتی به نسبت سادهتر و استاندارد مطرح شد. البته این بار سازمان سنجش از طرف دیگر بام افتاد!
در این مقاله تحلیل دقیقی بر سوالات کنکور خواهیم داشت و برای هر سوال کلید اولیهی سازمان سجش ارائه شده و سطح دشواری هر یک از سوالات را به صورت زیر بیان کردهایم:
- الف: ساده
- ب: متوسط
- ج: دشوار
- د: بسیار دشوار
لازم به ذکر است که تعیین سطح دشواری سوالات، کاملاً نظر شخصی بنده است و ممکن است دیگر اساتید و مشاوران نظر متفاوتی داشته باشند.
بررسی و تحلیل تک تک سوالات ریاضی کنکور تجربی ۱۴۰۱ داخل کشور
پیش از آن که به تحلیل سوالات بپردازیم بیان چند مورد زیر الزامی به نظر میرسد:
- دفترچهای که سوالات کنکور از آن برش داده شدهاند، دفترچهی کد ۲۲۱ – A است که در سایت سازمان سنجش منتشر شد.
- اگر در سوالی نظری متفاوت با کلید اولیهی سازمان سنجش داشتهام، در توضیحات سوال بیان کردهام.
- کیفیت عکسهای برش داده شده، پایین است و این به دلیل کیفیت پایین دفترچههای منتشر شده در سایت سازمان سنجش است؛ بابت این موضوع عذر ما را بپذیرید.
حال به تحلیل سوالات میپردازیم:

درجهی دشواری: ب
مبحث: توانهای گویا و عبارات جبری (فصل سوم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۲
سوال طوری طراحی شده که داوطلب نمیداند باید از کجا شروع به حل کند؛ اما اگر این ایده به ذهن او برسد که عبارت اول را با انتقال به مخرج، به عبارتی با توان مثبت تبدیل کند. همچنین با به توان ۲ رساندن عبارت زیر رادیکال فرجه ۲، آن را نیز به فرجه ۴ تبدیل کند، به سادگی با فاکتور گرفتن عدد ۲، عاملی مساوی با مخرج پدید میآید که بعد از سادهسازی به گزینهی ۲ میرسد.

درجهی دشواری: الف
مبحث: الگو و دنباله (فصل اول ریاضی دهم)
کلید اولیهی سازمان سنجش: ۴
برای من خیلی عجیب بود که چنین سوالی در کنکور ۱۴۰۱ مطرح شود. این سوال مشابه تمرینات کتاب درسی فصل اول ریاضی دهم است. برای حل هم کافی است فرمول الگوی خطی را بنویسید و با جایگذاری فرضیات مسئله به دستگاه دو معادله، دو مجهول برسید که با حل آن ضرایب به دست میآید و با یک جایگذاری ساده، جملهی شانزدهم را خواهید یافت. البته از آنجایی که هر الگوی خطی یک دنبالهی حسابی است، از فرمولهای دنبالهی حسابی نیز قابل حل خواهد بود.
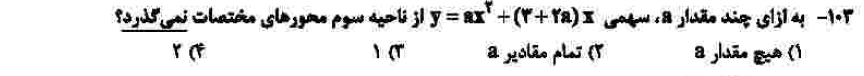
درجهی دشواری: ج
مبحث: تابع درجه دوم (فصل چهارم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۱
به نظرم سوال جذاب و خلاقانهای است. سطح دشواری ج برای این سوال به خاطر حل دشوار آن از روش عادی است. اما اگر داوطلب خلاقیت به خرج میداد و همچنین با دقت به صورت سوال، متوجه میشد که یکی از ریشهها صفر است؛ بنابراین سهمی از مبدا مختصات میگذرد و ریشهی دیگر نیز باید مثبت و تقعر سهمی رو به بالا باشد که از ناحیهی سوم عبور نکند (بنابراین باید ضریب x به توان ۲ یعنی a مثبت باشد). با فاکتورگیری از یک x، ریشهی دیگر بر حسب a به دست میآید که باید مثبت باشد، اما با توجه به توضیحات داده شده، آن ریشه همواره منفی است، پس به ازای هیچ مقداری از a درست نخواهد بود. اگر با این روش سوال حل شود سطح دشواری را میتوان حتی ب در نظر گرفت.

درجهی دشواری: ب
مبحث: ترکیب تعیین علامت و تابع جزصحیح (فصل چهارم ریاضی دهم و فصل سوم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۴
برای حل میتوانید با یک تعیین علامت ساده، نامعادله را حل کنید و بازهی x را به دست آورید. با ضرب آن در سه حدود 3x نیز به دست میآید که جزصحیح مقادیر این بازه، تعداد اعضا به سادگی پیدا خواهد شد.
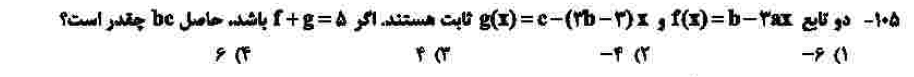
درجهی دشواری: الف
مبحث: تابع ثابت (فصل پنجم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۳
سوال پیش رو بسیار پرتکرار و ساده است. برای حل باید بدانیم که تابع ثابت، x ندارد، بنابراین ضرایب x در هر دو تابع صفر است که به سادگی a و b به دست میآیند. با استفاده از فرض دوم c نیز به دست میآید. طرح چنین سوالاتی بعد از کنکور طوفانی ۱۴۰۰ جای تعجب دارد!

درجهی دشواری: ب
مبحث: ترکیب انتقال توابع و فاصله دو نقطه (فصل پنجم ریاضی دهم و فصل اول ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۴
برای حل سادهتر بهتر است طول راس سهمی اول یعنی ۲ را به دست آوریم. سپس با انتقال داده شده در صورت سوال، راس سهمی دوم صفر خواهد شد. دو سهمی شبیه به هم داریم پس محل برخورد آنها وسط صفر و ۲ یعنی یک است. پس یک، طول نقطهی برخورد و عرض آن هم با جایگذاری در سهمی صورت سوال، ۳ به دست میآید که فاصلهی نقطهی (۳، ۱) از مبدا مختصات به سادگی به دست میآید.
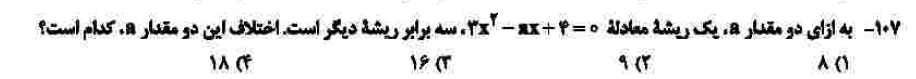
درجهی دشواری: ب
مبحث: روابط بین ریشههای معادله درجه دوم (فصل اول ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۳
در ظاهر سوال بسیار دشوار است، اما اگر داوطلب شروع به حل کند، میبیند که آنچنان هم دشوار نیست. دو ریشه را با توجه به صورت سوال میتوان m و 3m در نظر گرفت که از فرمول ضرب ریشهها، برای m دو مقدار به دست میآید. با فرمول جمع ریشهها و با استفاده از دو مقدار m، دو مقدار مختلف نیز برای a به دست میآید.

درجهی دشواری: د
مبحث: ترکیب معادلهی گویا و رادیکالی (گنگ) (فصل اول ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۳
این سوال را باید جز معدود سوالات بسیار دشوار این کنکور دانست. هرچند راهحلهای خلاقانهای نیز برای وجود داد که حل را سادهتر میکند. برای حل ابتدا سمت راست را ساده کنید، برای سمت چپ نیز در مخرج مشترک گیری از مزدوج بودن مخرجها استفاده کنید. با این کار حل سادهتر میشود؛ هرچند کماکان باید محاسبات گویا انجام دهید.

درجهی دشواری: الف
مبحث: تابع وارون (فصل سوم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: 2 نکتهی جالب دربارهای این سوال، یک به یک نبودن y است. برای مثال اگر اعداد صفر، یک و منفی یک را جایگذاری کنید، مقدار یک را دریافت میکنید که نشان از یک به یک نبودن و عدم وارونپذیری تابع است؛ بنابراین سوال غلط است. البته بعید است این سوال حذف شود زیرا با جابهجا کردن طول و عرض نقاط و جایگذاری در تابع فقط گزینهی 2 در آن صدق میکند.

درجهی دشواری: ب
مبحث: ترکیب توابع (فصل اول ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۴
شاید از اینکه سطح دشواری این سوال ب است، تعجب کرده باشید و اعتقاد داشته باشید که سوال دشوار است؛ اما باید بگویم حتی میشد سطح دشواری را الف نیز در نظر گرفت، زیرا در تابع gof تمامی تغییرات روی دامنه انجام شده که روی برد آن بیتاثیر است و کمترین مقدار تابع نیز از برد آن استخراج میشود. همانطور که میدانید کمترین مقدار تابع gof، 11 است، پس پاسخ سوال نیز 11 است.

درجهی دشواری: ب
مبحث: یکنوایی توابع (فصل اول ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۱
همانطور که میدانید تابع درجه سه (لر)، اکیدا صعودی است و زمانی نزولی میشود که ضریب آن منفی باشد. پس با حل یک نامعادلهی ساده، مقادیر k، مثبت و منفی یک، مثبت و منفی دو و صفر خواهد شد که مجموع آن صفر است. در ضمن عدد ۵ موجود در تابع، تاثیری در یکنوایی تابع ندارد و فقط تابع ۵ واحد به بالا منتقل میکند.
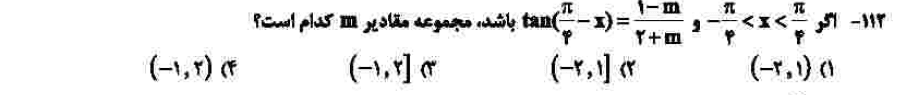
درجهی دشواری: ج
مبحث: حدود توابع مثلثاتی (فصل دوم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۱
سطح دشواری سوال از این بابت ج است که صورت سوال کمی ترسناک اما در حقیقت سوال سختی نیست. برای حل ابتدا حدود کمان مقابل تانژانت را مییابیم که بین صفر تا ۹۰ درجه خواهد شد. با توجه به نمودار تابع تانژانت در بازهی صفر تا ۹۰، مقادیر صفر تا مثبت بینهایت است پس باید نامعادلهای تشکیل دهید که مقدار آن مثبت و از آن حدود m را بیابید.

درجهی دشواری: الف
مبحث: اتحادهای مثلثاتی (فصل دوم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۳
برای حل سوال کافی است که یکی از سینوسها را جدا کنید و با کسینوس مقدار یک را بسازید تا مقدار سینوس به توان دو به دست آید و مقدار کسینوس به توان دو هم به سادگی یافت میشود. از تقسیم این دو بر هم، پاسخ سوال به دست میآید.
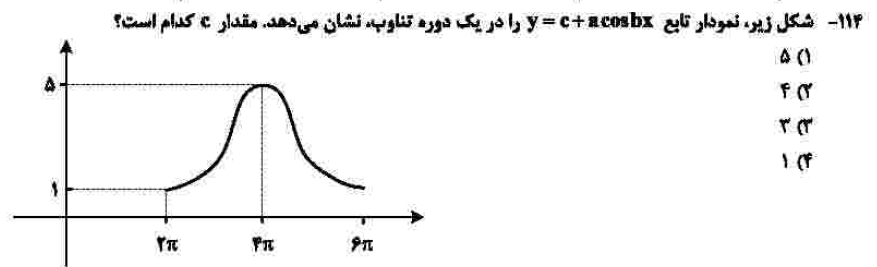
درجهی دشواری: الف
مبحث: نمودار توابع مثلثاتی (فصل دوم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۳
یکی از سادهترین سوالات کنکور همین بود. میانگین مقادیر ماکسیمم و مینیمم توابع سینوس و کسینوس، برابر با مقدار c است. یعنی میانگین ۱ و ۵ !!! مقادیر a و b در پاسخ بیتاثیر هستند. این کنکور هم با سوالات مثلثاتش ترکونده یعنی!!!
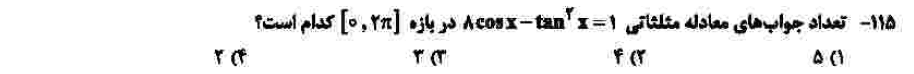
درجهی دشواری: ب
مبحث: معادلات مثلثاتی (فصل دوم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۴
برای حل این معادلهی سادهی مثلثاتی، تانژانت را به سمت راست میبریم که با استفاده از اتحادهای مثلثاتی، معادله را ساده کنیم، در نهایت مقدار کسینوس، یک دوم خواهد شد که در یک دورهی تناوب دو جواب دارد! به همین سادگی! خیلی با ارفاق سطح دشواری سوال ب است.
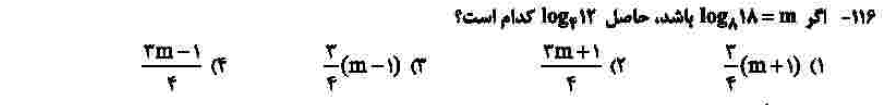
درجهی دشواری: ج
مبحث: لگاریتم (فصل پنجم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۱
از معدود سوالات این کنکور بود که ارزش بحث کردن دارد. برای حل باید لگاریتم ۳ در مبنای ۲ را از فرض به دست آورید و برای به دست آوردن پاسخ سوال از آن استفاده کنید.

درجهی دشواری: الف
مبحث: توابع نمایی (فصل پنجم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۳
با جایگذاری نقاط (0، 0) و (۱-، ۱-) در تابع، یک دستگاه دو معادله دو مجهول برای یافتن مقادیر a و b خواهید داشت که به سادگی پاسخ به دست میآید. نکتهی جالب و حتی طنز سوال اینجاست که نقطهی داده شده در تابع معکوس طول و عرض برابر دارد و حتی اگر داوطلب متوجه معکوس بودن آن هم نشود، میتواند پاسخ درست به دست آورد.

درجهی دشواری: الف
مبحث: آمار، معیارهای پراکندگی (فصل هفتم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۴
این سوال حتی با نگاه هم قابل حل است! برای به دست آوردن واریانس، میانگین مجذور اختلاف دادهها از میانگین را مییابیم. یعنی ۸ تا یک و منفی یک به توان دو برسند و در نهایت با هم جمع شوند مقدار ۸ خواهد شد که باید بر ۹ یعنی تعداد دادهها تقسیم شود. در نهایت انحراف معیار، جذر واریانس است.

درجهی دشواری: الف
مبحث: آمار، معیارهای گرایش به مرکز (فصل هفتم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۱
این سوال از قبلی هم سادهتر است. میدانیم که هر عملیات ریاضی روی دادهها انجام دهیم، همان عملیات هم روی میانگین و میانهی آنها نیز اجرا میشود، پس دو واحد به هر کدام از این دو اضافه میشود. از طرف دیگر میانگین و میانهی چند عدد متوالی، در صورت فرد بودن تعداد دادهها عدد وسط و یا در صورت زوج بودن تعداد دادهها، میانگین دو عدد وسط خواهد شد، پس با هم برابرند و اختلاف آنها صفر است. دو سوال متوالی با نگاه حل میشوند، عجیب نیست؟!

درجهی دشواری: الف
مبحث: حد و پیوستگی (فصل ششم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۲
برای حل این سوال ساده کافی است مقدار جزصحیح که ۸ است را به دست آورید. پس از آن با یک حد مبهم سادهی صفرصفرم مواجه هستید که میتوانید با هوپیتال و یا اتحادها آن را رفع ابهام کنید و به پاسخ برسید.
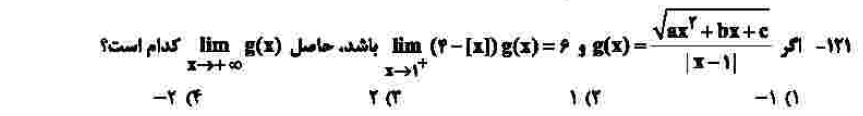
درجهی دشواری: ج
مبحث: حد در بینهایت و حد بینهایت (فصل سوم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۳
ابتدا با استفاده از فرض دوم سوال میتوان فهمید مقدار حد تابع g در سمت راست یک، برابر ۲ خواهد بود. با همین فرض میتوان فهمید که صورت این تابع نیز باید مانند مخرج صفر شود که در نهایت به این میرسیم که تابع g تابعی ثابت با برد ۲ است که حد آن در بینهایت هم ۲ میشود.
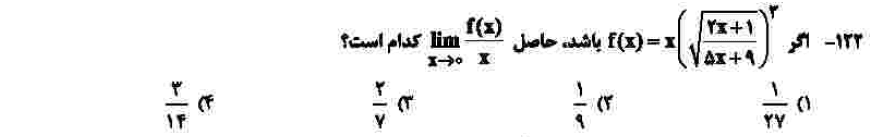
درجهی دشواری: الف
مبحث: حد و پیوستگی (فصل ششم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۱
احساس من بر این است که طراح فقط قصد داشته با ظاهر سخت سوال، دانشآموز را بترساند. اما جالب است که x تابع f با x مخرج حد خواسته شده ساده میشود و سوال با یک جایگذاری بسیار ساده حل میشود. حتی صفرصفرم هم نمیشود. به نظرم با نگاه هم قابل حل بود.

درجهی دشواری: ج
مبحث: مشتق، خط مماس بر منحنی (فصل چهارم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۴
این سوال، از سوالات خوب این آزمون بود. ابتدا باید بدانید واحد، به معنای یک است. نکته دیگر اینکه در نقطهی تماس خط مماس و منحنی، هم مقدار مشتق آنها و هم مقدار عرض آنها برابر است. این موضوع کلید حل این سوال دشوار است.
درجهی دشواری: ج
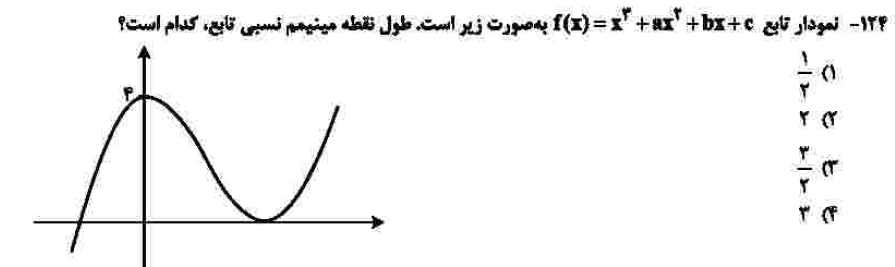
مبحث: کاربرد مشتق، اکسترممهای نسبی (فصل پنجم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: 2
برای حل این سوال باید ابتدا مشتق بگیریم و میدانیم مشتق در صفر، صفر خواهد شد، چون در صفر ماکسیمم نسبی دارد؛ پس مقدار b صفر میشود. با نگاهی به تابع، c نیز 4 میشود. ریشهی دیگر مشتق همان طول نقطهی مینیمم نسبی که با جایگذاری آن در خود تابع، عرض آن باید صفر شود. با این کار مقدار a نیز به دست میآید و با جایگذاری در طول مینیمم نسبی، حاصل به دست میآید.

درجهی دشواری: ب
مبحث: کاربرد مشتق، بهینهسازی (فصل پنجم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۲
مانند همهی سوالات بهینهسازی باید تابعی که بیشترین یا کمترین مقدار آن خواسته شده است را بنویسیم. پس تابع حجم مخروط را مینویسیم و با استفاده از اطلاعات سوال آن را تکمتغیره میکنیم، مشتق میگیریم و برابر صفر قرار میدهیم. مقدار ارتفاع به دست آمده بعد از حل معادلهی مشتق برابر صفر، پاسخ مسئله است.

درجهی دشواری: د
مبحث: شمارش، بدون شمردن (فصل ششم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۳
من به صورت این سوال انتقاد دارم، زیرا خیلی واضح نیست. به نظر میشد که بهتر بیان شود. اما در هر حال باید حالتبندی کنید، مثلاً یکی از حالتها این است که ریاضی و زیست انتخاب شوند، اما فیزیک انتخاب نشود، یا اینکه فیزیک انتخاب شود اما ریاضی و زیست انتخاب نشوند و دو حالت دیگر هم باید بنویسیم. مجموع تعداد این حالات پاسخ سوال است.

درجهی دشواری: الف
مبحث: قانون احتمال کل (فصل هفتم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۴
خیلی ساده باید دو عدد داده شده را در هم ضرب کنیم. فقط مراقب باشد در نهایت درصد احتمال خواسته شده است و باید عدد به دست آمده را در ۱۰۰ ضرب کنید. همین!!
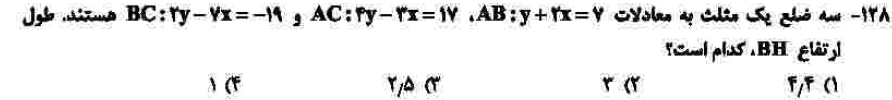
درجهی دشواری: ب
مبحث: هندسه تحلیلی (فصل اول ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۱
این سوال به نسبت سوالات دیگر زمان بیشتری میخواهد اما خیلی سخت نیست. برای به دست آوردن طول ارتفاع BH باید ابتدا نقطهی B که تقاطع خطوط BC و AB است را به دست آوریم و فاصلهی آن را از خط BC که از فرمول فاصلهی نقطه از خط به دست میآید، محاسبه کنیم.

درجهی دشواری: ب
مبحث: هندسه، قضیه تالس (فصل دوم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۴ دو مثلث مذکور در صورت سوال دارای ارتفاع برابر هستند، پس نسبت مساحت آنها برابر با نسبت قاعدههای آنها یعنی DE و BC برابر است. برای یافتن این نسبت کافی است یک تالس جز به کل در مثلث ABC بنویسید.

درجهی دشواری: ب
مبحث: هندسه، مقاطع مخروطی (فصل ششم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۱
با ارفاق سطح این سوال را ب در نظر گرفتم، به نظرم سوال سادهای است. برای حل مقادیر b و c به سادگی از صورت سوال استخراج میشوند که b برابر ۹ و c برابر ۱۲ میشود. از فرمول فیثاغورس معروف بیضی a هم ۱۵ به دست میآید. خروج از مرکز بیضی میشود c تقسیم بر a، یعنی ۱۲ تقسیم بر ۱۵ که حاصل هشت دهم و گزینهی ۲ است. پس کلید سازمان سنجش، اشتباه است.
جمعبندی و مقایسه با کنکور ۱۴۰۰
برای جمعبندی دقیقتر باید به جدول درجهی دشواری زیر بنگریم:
| سطح | ساده | متوسط | دشوار | بسیار دشوار |
| تعداد | ۱۱ | ۱۱ | ۶ | ۲ |
میبینید که یک دانشآموز سطح پایین، اگر سوالات ساده کنکور ۱۴۰۱ را در جلسه پیدا میکرد، میتوانست ۳۵ درصد پاسخ دهد، در صورتی که در کنکور ۱۴۰۰، ۳۵ درصد، درصد بسیار خوبی تلقی میشد. برای این که حرف مرا بهتر متوجه شوید، به جدول زیر، که درجهی دشواری سوالات ریاضی کنکور تجربی ۱۴۰۰ داخل کشور را نشان میدهد، بنگرید.
| سطح | ساده | متوسط | دشوار | بسیار دشوار |
| تعداد | ۲ | ۹ | ۱۴ | ۵ |
قضاوت با خودتان!

