کنکور ۱۴۰۱ هم مانند همهی کنکورهای سالهای گذشته با همهی فراز و نشیبهایی که داشت برگزار شد. چیزی که واضح و مبرهن است، سطح دشواری سوالات درس ریاضی در رشتهی تجربی نسبت به کنکور سراسری ۱۴۰۰ بسیار سادهتر شده بود. جالبتر این که در حدی سوالات ساده شده بود که کمتر کسی این پیشبینی را میتوانست داشته باشد. برخی از اساتید مطرح ریاضی کشور در صفحهی اینستاگرام خود، از سوالات ریاضی تجربی ۱۴۰۱، به عنوان یک شوخی یاد کرده بودند. من نیز این را به حساب غافلگیریهای سازمان سنجش برای داوطلبان کنکور، که سالهای پیش نیز سابقه داشته، میگذارم. در این مطلب قصد دارم که به بررسی تک تک سوالات کنکور در درس ریاضی رشتهی تجربی خارج از کشور سال ۱۴۰۱ بپردازم. برای هر سوال سطح دشواری سوالات را نیز به از الف تا د به ترتیب زیر ارائه دادهام:
- الف: ساده
- ب: متوسط
- ج: دشوار
- د: بسیار دشوار
لازم میدانم که این موضوع را نیز قید کنم که تعیین سطح دشواری سوالات نظر شخصی من است و میتواند با نظر سایر افراد متخصص در این زمینه متفاوت باشد.
بررسی و تحلیل تک تک سوالات ریاضی کنکور تجربی ۱۴۰۱ خارج از کشور
قبل از شروع تحلیل، یادآور میشوم که:
- سوالات زیر از دفترچهی کد 261 – A که در سایت سازمان سنجش منتشر شده، استخراج شده است.
- برای هر سوال کلید اولیهی سازمان سنجش هم ارائه شده است. اگر در سوالی نظری متفاوت با این کلید داشتهام، بیان کردهام.
- کیفیت پایین سوالات به دلیل کیفیت پایین دفترچهی بارگذاری شده در سایت سازمان سنجش است.
در ادامه تحلیل سوالات را خواهید دید.
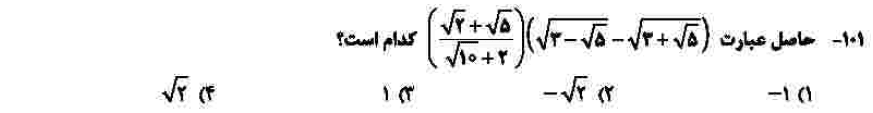
درجهی دشواری: ب
مبحث: توانهای گویا و عبارات جبری (فصل سوم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۱
این سوال بسیار پرتکرار است و از مشابه آن در سوالات داخل کشور سادهتر است. برای حل، هر پرانتز را جدا بررسی میکنیم. در پرانتز اول باید از مخرج، رادیکال 2 فاکتور بگیرید که با صورت ساده شود. پرانتز دوم را ابتدا به توان دو میرسانیم که محاسبهی آن سادهتر شود، سپس از پاسخ جذر میگیریم. دام سوال در این است که در پرانتز دوم مقدار منفی است، باید مراقب باشید که بعد از جذر گرفتن، مقدار منفی قابل قبول است.

درجهی دشواری: ج
مبحث: الگو و دنباله (فصل اول ریاضی دهم)
کلید اولیهی سازمان سنجش: ۴
سوال دوم این کنکور، سوالی بود که باید محاسبات زیادی را برای حل آن انجام دهیم. محاسبات آن سخت و پیچیده نیست، اما زمانبر است. برای حل باید یک دنبالهی درجه دوم در نظر بگیریم و اطلاعات داده شده را روی آن پیاده کنیم تا ضرایب b و c به دست آیند. درجهی دشواری ج به دلیل حجم محاسبات است.
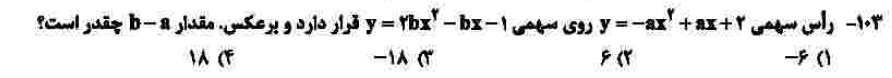
درجهی دشواری: ب
مبحث: تابع درجه دوم (فصل چهارم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۲ برای این سوال باید طول و عرض راس هر کدام از سهمیها را یافت و در سهمی دیگر جایگذاری کرد. با این کار ابتدا a و سپس b به دست میآید. سختی این سوال در محاسبات کسری و نسبتاً طولانی آن نهفته است.

درجهی دشواری: ب
مبحث: ترکیب تعیین علامت و تابع جزصحیح (فصل چهارم ریاضی دهم و فصل سوم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۲
برای حل ابتدا باید x را در معادلهی اولیه به دست آورید. سپس با ضرب نامعادله در یک دوم، بازهی مقدار درون جزصحیح را بیابید. با جزصحیح گیری از آن به سادگی تعداد اعضای صحیح به دست میآید.

درجهی دشواری: الف
مبحث: تابع ثابت (فصل پنجم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۳
میدانیم که تابع ثابت، تابعی است که برد آن فقط یک عضو دارد و در ضابطهی آن x وجود ندارد. بر همین اساس باید برای حل ابتدا با ضرب پرانتزها و استاندارد کردن آن، ضرایب عبارتی که x دارند را صفر قرار داد و a و b را یافت. مقدار 2b با توجه به ضابطه، پاسخ سوال است.

درجهی دشواری: ج
مبحث: ترکیب انتقال توابع و فاصله دو نقطه (فصل پنجم ریاضی دهم و فصل اول ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۴
ابتدا باید تغییرات بیان شده را روی f اعمال کنید که تابع جدید به دست آید. سپس تابع جدید را با f برابر قرار میدهیم، که برای x دو مقدار قرینه به دست میآید و با جایگذاری، عرض نقطهی برخورد را به دست میآوریم. جالب است که معادلهی به دست آمده یک معادلهی گویا است. فاصلهی نقطهی برخورد با مبدا پاسخ سوال است. در ضمن فاصلهی هر دو نقطهی به دست آمده از معادله با مبدا مختصات، به دلیل قرینه بودن آنها، برابر است و پاسخ سوال یکتا است.
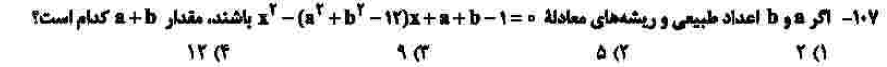
درجهی دشواری: ب
مبحث: روابط بین ریشههای معادله درجه دوم (فصل اول ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۲
ظاهر سوال، دشوار به نظر میرسد. اما کافی است که از روابط بین ریشهها استفاده کنید و s که همان a + b و p که همان ab است را با استفاده از معادلهی داده شده به دست آورید. سپس با جایگذاری s و p در روابط، مقدار s که پاسخ سوال است را بیابید.

درجهی دشواری: ج
مبحث: ترکیب معادلهی گویا و رادیکالی (گنگ) (فصل اول ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۱
ظاهر سوال، نوید سوالی دشوار را میدهد. برای حل ابتدا سمت راست معادله را ساده میکنیم. سپس برای سمت چپ مخرج مشترک میگیریم و برای سادگی حتما از مزدوج بودن مخرجها استفاده کنید. با حل معادله به هیچ ریشهی مثبتی نمیرسیم.
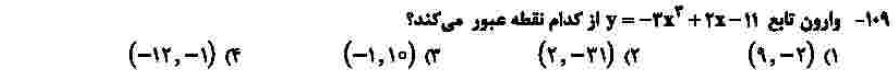
درجهی دشواری: الف
مبحث: تابع وارون (فصل سوم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۱
طراحان سوالات ریاضی کنکور تجربی ۱۴۰۱ هم در سوالات داخل کشور و هم در سوالات خارج از کشور، سوال ۱۰۹ را اشتباه طرح کردهاند. اگر تابع درجه سوم صورت سوال را با استفاده از نقطهیابی رسم کنید، میبینید که یک به یک نیست و در نتیجه وارونپذیر نیست. اما دور از انتظار است که این سوال حذف شود. بنابراین دانشآموزان باید با استفاده از تعریف وارون تابع، جای طول و عرض نقاط موجود در گزینهها را عوض کنند و در تابع جایگذاری کنند، هر کدام که صدق کرد، پاسخ سوال است.

درجهی دشواری: ب
مبحث: ترکیب تابع وارون و ترکیب توابع (فصل سوم ریاضی یازدهم و فصل اول ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۲
سه تابع خطی در شکل دیده میشود که باید ضابطهی هر کدام را بیابید. توجه کنید که تابع g دو ضابطه دارد. با جایگذاری ساده، حاصل به دست میآید. به نظر اگر دانشآموزی اقدام به حل میکرد، میتوانست با صرف زمانی حدود ۲ دقیقه به پاسخ برسد.

درجهی دشواری: ج
مبحث: ترکیب تعیین علامت و یکنوایی توابع (فصل چهارم ریاضی دهم و فصل اول ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۴
سوال هوشمندانه و مفهومی است. باید هر کدام از عبارات زیر رادیکال را جداگانه تعیین علامت کنید. علامت تابع f با توجه به نزولی اکید بودنش تا قبل از 3، مثبت و بعد از 3 منفی خواهد شد. عبارت دیگر زیر رادیکال هم که در صفر، صفر میشود و در دیگر بازهها مثبت است. با کشیدن یک جدول تعیین علامت، مشخص میشود که ۴ عدد با ویژگی خواسته شده موجود است.

درجهی دشواری: ج
مبحث: حدود توابع مثلثاتی (فصل دوم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۲
برای حل این سوال باید ابتدا حدود 2x را بیابید و با رسم این حدود در دایره مثلثاتی، حدود sin 2x را پیدا کنید. با این حدود میتوانید حدود m را نیز به دست آورید. حل این سوال نیازمند درک درست از نسبتهای مثلثاتی است.
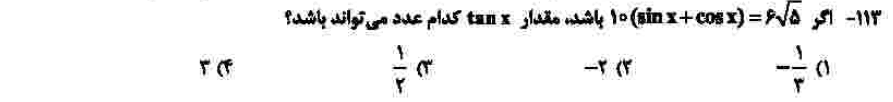
درجهی دشواری: ب
مبحث: اتحادهای مثلثاتی (فصل دوم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۳
برای حل این سوال ابتدا باید طرفین را بر ۱۰ تقسیم کنیم، سپس با به توان رساندن طرفین مقدار sin 2x را بیابیم. با روابط مثلثاتی، از روشهای متفاوتی میتوان به پاسخ مسئله رسید.

درجهی دشواری: ب
مبحث: نمودار توابع مثلثاتی (فصل دوم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۴
برای حل این سوال ابتدا میتوانیم c که میانگین ماکسیمم و مینیمم است را به دست آوریم و در نهایت یک میشود. با توجه به دورهی تناوب، b نیز ۲ میشود. با جایگذاری نقطهی ماکسیمم در تابع، میتوانیم a که منفی سه دوم میشود را بیابیم. در نهایت پاسخ حاصل ضرب a و c است.

درجهی دشواری: ب
مبحث: معادلات مثلثاتی (فصل دوم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۲
ابتدا با استفاده از کمان پی دوم، sin را به cos تبدیل میکنیم. با ضرب کمان cos در منفی، که منفی در کمان آن بیتاثیر است، دو cos با کمان برابر داریم که میتوانیم آن به صورت مجذور بنویسیم. در نهایت مقدار cos با یک و منفی یک برابر میشود که در بازهی داده شده دو جواب دارد.
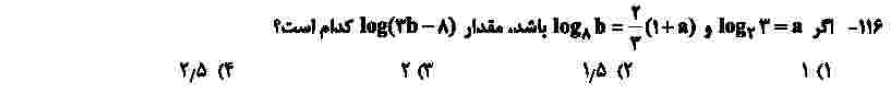
درجهی دشواری: ب
مبحث: لگاریتم (فصل پنجم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۳
سوال خیلی دشواری نیست و برای حل باید با استفاده از ضریب دو سوم، a را در مبنای ۸ نوشت و با استفاده از قواعد لگاریتم b را مییابیم که مقدار آن 36 میشود. با جایگذای آن، حاصل خواستهی سوال ۲ خواهد شد.
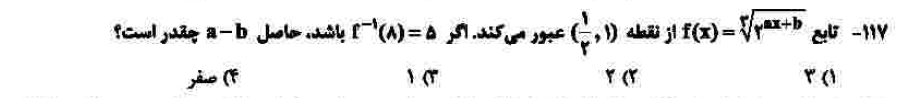
درجهی دشواری: ب
مبحث: ترکیب توابع نمایی و رادیکالی (فصل سوم و پنجم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۱
برای حل این سوال ابتدا با جایگذاری نقطهی داده شده و با جایگذاری نقطهی (8، 5) که بعد از جابجایی طول و عرض به دلیل وارون بودن آن به دست میآید، دستگاه دو معادله دو مجهول خواهیم داشت، که a و b را از حل آن مییابیم.

درجهی دشواری: ب
مبحث: آمار، معیارهای پراکندگی (فصل هفتم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۴
ابتدا میدانیم که مجموع اختلاف دادهها از میانگین برابر صفر است. در این صورت مجموع a و b برابر منفی یک میشود. واریانس دادهها، مجذور انحراف معیار یعنی ۴ است. با توجه به این که تعداد دادهها شش است، صورت واریانس برابر 24 میشود. پس مجموع مجذور اختلافها از میانگین ۲۴ خواهد شد. در ادامه مجموع مجذور a و b، ۱۳ میشود، با توجه به مثبت بودن a، مقدار b، منفی سه خواهد شد.

درجهی دشواری: ج
مبحث: آمار، معیارهای گرایش به مرکز (فصل هفتم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۳
فهم صورت سوال، شاید سختترین قسمت حل باشد. یکی از راهحلهای خلاقانه برای این سوال است که بدانیم چارک دوم همان میانه است و قطعا میانگین دادههای کوچکتر از میانه، کمتر یا مساوی میانه است و میانگین دادههای بیشتر از میانه بیشتر یا مساوی میانه است. طبق اطلاعات داده شده، میتوانیم برای دادههای کمتر و بیشتر از میانه دو میانگین حدس بزنیم که ۲ و ۴ هستند. چون قرینهی ۲، ۶ واحد از ۴ کمتر است. از آنجایی که تعداد دادهها زوج است، میانگین کل دادهها با میانگین ۲ و ۴ برابر است.
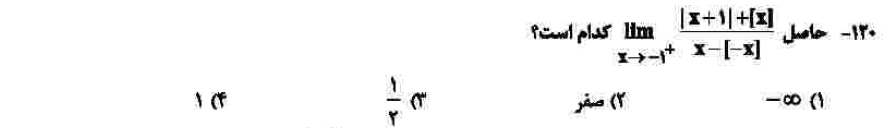
درجهی دشواری: الف
مبحث: حد و پیوستگی (فصل ششم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۴
برای حل باید قدرمطلق را تعیین علامت کنیم که مثبت است و خود عبارت از آن بیرون میآید. جزصحیح صورت برابر منفی یک شده و جزصحیح مخرج صفر میشود، پس به کسر x بر روی x میرسیم که حاصل یک است.

درجهی دشواری: ج
مبحث: حد در بینهایت (فصل سوم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۱
در نوع خود سوال جالبی است. با نگاهی به حدی که به بینهایت میل میکند، متوجه میشویم باید ضریب x در تابع f، یک دوم باشد؛ پس با توجه به رادیکال تابع f، a برابر یک چهارم خواهد شد. مقدار جزصحیح در خواستهی سوال برابر منفی یک میشود که به دست آوردن آن نیاز به دقت زیادی دارد. همچنین حد تابع f در سمت چپ منفی یک، برابر یک دوم خواهد شد.
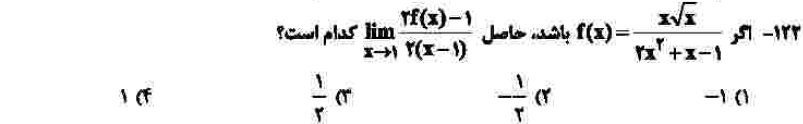
درجهی دشواری: ج
مبحث: حد و پیوستگی (فصل ششم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۲
همانطور که میبینید، حد تابع f در یک، برابر یک دوم خواهد شد و با جایگذاری آن در حد خواسته شده، به صفر صفرم میرسیم، برای رفع ابهام باید هوپیتال بگیریم که نیازمند مقدار مشتق تابع f در یک خواهیم شد. شاید مشتقگیری از آن کمی دشوار باشد، اما راهحل بهتری را برای آن متصور نیستم.

درجهی دشواری: ج
مبحث: مشتق، خط مماس بر منحنی (فصل چهارم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۳
میدانیم در نقطهی تماس خط مماس بر تابع، هر دو هم دارای مشتق برابر و هم دارای عرض برابر هستند. واحد هم که به معنای یک است. اگر مقدار عرض هر دو تابع را در یک حساب کنیم، b برابر با منفی یک میشود. مشتق خط مماس برابر ۲ است، پس مشتق y نیز در یک، برابر ۲ میشود. با حل این معادله دو مقدار برای a به دست میآید که مقدار منفی یک آن، چون مخرج را در طول یک، صفر میکند؛ قابل قبول نیست.

درجهی دشواری: ب
مبحث: کاربرد مشتق، اکسترممهای نسبی (فصل پنجم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۱
این سوال محاسبات نسبتاً طولانی دارد، اما ساده است. برای حل مشتق میگیریم و با جایگذاری مقادیر صفر و منفی دو در مشتق باید به صفر برسیم؛ زیرا در اکسترممهای نسبی تابع درجه سوم، مماس افقی داریم که شیب آن صفر است. با حل دستگاه دو معادله دو مجهول، مقادیر a و b به دست میآید. که با جایگذاری این دو مقدار در تابع اصلی، عرض نقاط اکسترمم نسبی را هم مییابیم. فاصلهی دو نقطهی به دست آمده پاسخ سوال است.

درجهی دشواری: ب
مبحث: کاربرد مشتق، بهینهسازی (فصل پنجم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۲
همانند همهی سوالات بهینهسازی ابتدا تابع مساحت حلب استفاده شده را مینویسیم و با استفاده از مقدار حجم، یکی از متغیرها را بر حسب دیگری مییابیم و تابع مساحت حلب استفاده شده را تک متغیره میکنیم. با مشتقگیری و برابر صفر قرار دادن تابع مشتق، متغیرها را مییابیم و با جایگذاری آن در تابع مساحت حلب استفاده شده، حاصل را پیدا میکنیم.

درجهی دشواری: ج
مبحث: شمارش، بدون شمردن (فصل ششم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۳
کتابهای وسط (بجز اول و آخر) با توجه به صورت سوال باید یک در میان باشند، که در نوع خود سوال جدیدی محسوب میشود. با توجه به این که تعداد کتابهای ریاضی بیشتر است، پس مجبوریم که کتابهای اول و آخر را ریاضی بگذاریم و دو حالت زیر به وجود میآید:
حالت اول: (ر – ر – آ – ر – آ – ر) که میشود: 48 = !4 × !2
حالت دوم: (ر – آ – ر – آ – ر – ر) که میشود: 48 = !4 × !2
پس در کل ۹۶ حالت داریم که گزینهی ۱ پاسخ سوال است اما در کلید اولیهی سازمان سنجش گزینهی ۳ ارائه شده؛ بنابراین به نظر من کلید اشتباه است.

درجهی دشواری: ج
مبحث: قانون احتمال کل (فصل هفتم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۴
سوالی که میبینید ممکن است با هر راهحل یکی از پاسخهای موجود در گزینهها به دست آید، بنابراین برای حل باید دقت بسیاری کنید. بهترین روش نمودار درختی است. در نمودار درختی به احتمال یک چهارم هر دو پشت خواهد آمد که به احتمال یک دوم سکهی بعدی رو خواهد بود، پس تا اینجا یک هشتم. به احتمال یک چهارم هر دو رو خواهد آمد که سکهی بعدی هر چه بیاید، شرایط مطلوب سوال نیست پس این حالت احتمال صفر دارد. به احتمال یک دوم سکهها متفاوت خواهند شد، پس برای شرایط مطلوب، باید در دو سکهی دیگر، یکی رو و دیگری پشت بیاید که این هم یک دوم خواهد و یک چهارم به دست میآید. جمع یک چهارم و یک هشتم، سه هشتم میشود.
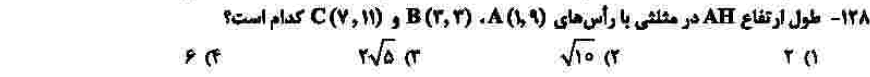
درجهی دشواری: الف
مبحث: هندسه تحلیلی (فصل اول ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۳
سوال بسیار سادهای است که برای حل باید فاصلهی نقطهی A را از خط BC به دست آورید. پس با نوشتن معادلهی خط BC و فرمول فاصلهی نقطه از خط، به سادگی به جواب میرسیم.

درجهی دشواری: الف
مبحث: هندسه، قضیه تالس (فصل دوم ریاضی یازدهم)
کلید اولیهی سازمان سنجش: ۴
اگر باهوش باشید متوجه خواهید شد که قاعدهی هر دو مثلث، خط DE و با توجه به موازی بودن دو خط DE و BC ارتفاع آنها نیز برابر خواهد شد، پس مساحتها برابر است.
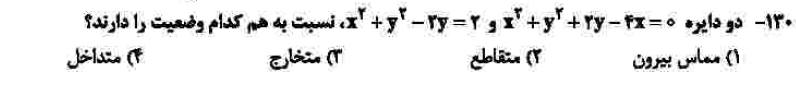
درجهی دشواری: ب
مبحث: هندسه، مقاطع مخروطی (فصل ششم ریاضی دوازدهم)
کلید اولیهی سازمان سنجش: ۲
در هر دو دایره باید مراکز و شعاعها را یافت. چون فاصلهی دو مرکز بیشتر از اختلاف شعاعها و کمتر از مجموع شعاعها است؛ بنابراین دو دایره متقاطعاند. سطح دشواری ب به دلیل محاسبات نسبتاً زمانبر است؛ ولی این سوال مشابه تمرینات کتاب درسی است.
جمعبندی و مقایسه با کنکور ۱۴۰۱ داخل کشور تجربی
در جدول زیر سطح سوالات را به صورت کلی میبینید.
| سطح | ساده | متوسط | دشوار | بسیار دشوار |
| تعداد | ۵ | ۱۴ | ۱۱ | ۰ |
به نظر میرسد که با این آمار باید بگوییم سوالات این آزمون استاندارد بوده و دانشآموزان متوسط و حتی ضعیفتر میتوانستند حداقل به ۱۰ سوال پاسخ دهند که درصد ۳۳ را برای آنها به ارمغان میآورد. خالی از لطف نیست که این کنکور را با سوالات داخل کشور مقایسه کنیم. جدول زیر، آمار کلی سوالات ریاضی داخل کشور کنکور ۱۴۰۱ است.
| سطح | ساده | متوسط | دشوار | بسیار دشوار |
| تعداد | ۱۱ | ۱۱ | ۶ | ۲ |
همانطور که میبینید تعداد سوالات سادهی داخل کشور بسیار بیشتر است، اما در عوض سوالات دشوار کمتری دارد. در کنکور خارج کشور نیز هیچ سوال بسیار دشواری وجود ندارد و در مقابل، داخل کشور ۲ سوال بسیار دشوار دارد. با این اوصاف باید کنکور خارج کشور را از نظر سوالات ریاضی، آزمون متعادلتری بدانیم.

