در کنکور ۱۴۰۱ برای اولین بار در رشتهی ریاضی، درس ریاضی از دروس فیزیک و شیمی جدا شد و دارای دفترچه و پاسخنامه مجزا بود. تعداد سوالات از ۵۵ به ۵۰ و زمان حل سوالات از ۸۵ به ۸۰ کاهش یافت. بنابراین دانشآموز نمیتوانست وقت ریاضی را به دروس فیزیک و شیمی بدهد و برعکس. در این مقاله قصد دارم که سوالات حسابان و ریاضی پایه کنکور ریاضی ۱۴۰۱ داخل کشور را تحلیل کنم و برای هر سوال یکی از سطوح زیر را برای مشخص شدن میزان دشواری آن، بیان کنم.
- الف: ساده
- ب: متوسط
- ج: دشوار
- د: بسیار دشوار
در ضمن تعیین سطح دشواری، نظر شخصی است و افراد دیگر ممکن است نظر متفاوتی داشته باشند. مباحث زیر جز حسابان و ریاضی پایه محسوب میشوند:
- کل کتاب ریاضی دهم به جز دروس اول و دوم فصل اول (مجموعهها)، فصل ششم (شمارش، بدون شمردن) و فصل هفتم (آمار و احتمال)
- کل کتاب حسابان یازدهم
- کل کتاب حسابان دوازدهم
بررسی و تحلیل تک تک سوالات حسابان و ریاضی پایه کنکور ریاضی ۱۴۰۱ داخل کشور
قبل از این که به تحلیل سوالات بپردازم، توجه کنید که سوالات زیر از دفترچهی کد A – 121 برش داده شده که در سایت سازمان سنجش منتشر شده است. کیفیت پایین سوالات نیز به دلیل بیکیفیت بودن دفترچهی بارگذاری شده در سایت سازمان سنجش است.

درجهی دشواری: ج
مبحث: الگو و دنباله (فصل اول ریاضی دهم)
کلید اولیهی سازمان سنجش: ۴
دشوار بودن این سوال به دلیل جدید بودن آن است که برای حل، دانشآموز باید خلاقیت به خرج دهد. یکی از روشها نوشتن دنبالهها است که ممکن است دانشآموز تعدادی از دنبالهها را فراموش کند. در هر حال، دنبالههای زیر قابل قبول هستند:
دنبالهی اول: 1، 2، 4، 8، 16
دنبالهی دوم: 2، 4، 8، 16، 32
دنبالهی سوم: 3، 6، 12، 24، 48
دنبالهی چهارم: 4، 8، 16، 32، 64
دنبالهی پنجم: 5، 10، 20، 40، 80
دنبالهی ششم: 6، 12، 24، 48، 96
دنبالهی هفتم: 1، 3، 9، 27، 81
روش دیگر این است که میدانیم q به توان ۴، ضریب جملهی اول در جملهی پنجم است. پس q میتواند اعداد ۲ و ۳ باشد. با فرض q = ۲، جملهی اول، اعداد ۱، ۲، ۳، ۴، ۵ و ۶ میتواند باشد و با فرض q = ۳، جملهی اول، عدد ۱ میتواند باشد. پس در نهایت ۷ دنباله با این ویژگیها داریم.

درجهی دشواری: ب
مبحث: تابع درجه دوم (فصل چهارم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۱
سوال سادهای نیست. میدانیم کمترین مقدار سهمی در راس آن اتفاق میافتد. عرض راس سهمی با دو برابر است. پس منفی دلتا بر روی 4a که همان عرض راس سهمی است را با ۲ برابر قرار میدهیم. معادلهی درجه دومی به دست میآید که m مثبت قابل قبول است زیرا باید ضریب x به توان دو مثبت باشد تا سهمی دارای کمترین مقدار باشد. با جایگذاری m در ضابطهی سهمی، معادلهی محور تقارن سهمی را که برابر با منفی b بر روی 2a است را مییابیم.

درجهی دشواری: د
مبحث: روابط بین ریشههای معادله درجه دوم (فصل اول حسابان یازدهم)
کلید اولیهی سازمان سنجش: ۱
این سوال از سوالات جدید این آزمون است که تقریباً نمونهی آن در جایی دیده نشده. روشهای متعددی برای حل آن وجود دارد. یکی از راهحلها، مربع کامل کردن معادله است که ریشههای کوچک و بزرگ مشخص شوند. با این روش میتوانیم جای آلفا و بتا عددی با یک مجهول بگذاریم و سوال را حل کنیم.
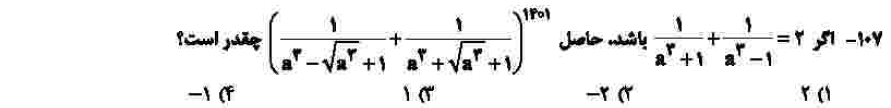
درجهی دشواری: ج
مبحث: ترکیب توانهای گویا و معادلات گویا (فصل سوم ریاضی دهم و فصل اول حسابان یازدهم)
کلید اولیهی سازمان سنجش: ۳
برای حل این سوال خلاقیتی که دانشآموز باید به خرج دهد، کامل حل نکردن معادله اول است. با مخرج مشترک گیری از معادله اول باید به عبارت a به توان ۶ برابر با a به توان 3 بهاضافه یک برسید. با مخرج مشترک گیری از عبارت داده شده که مزدوج هستند، باید به جای تمام a به توان 6ها، a به توان 3 بهاضافه یک قرار دهید که حاصل یک میشود. یک هم به توان هر عددی یک میشود. البته دانشآموز اگر باهوش باشد باید با توجه به توان ۱۴۰۱ سریعاً ۲ و منفی ۲ را حذف کند.

درجهی دشواری: ب
مبحث: یکنوایی توابع و توابع وارون (فصل دوم حسابان یازدهم و فصل اول حسابان دوازدهم)
کلید اولیهی سازمان سنجش: ۴
با ساده کردن رادیکال، به یک عبارت درجه سه میرسیم که به ازای xهای مثبت صعودی (به دلیل داشتن ضریب مثبت) و به ازای xهای منفی نزولی (به دلیل داشتن ضریب مثبت) است. پس باید وارون تابع را در xهای منفی به دست آوریم. دقت کنید برد تابع f همواره نامنفی، پس دامنهی معکوس آن هم همواره نامنفی است.
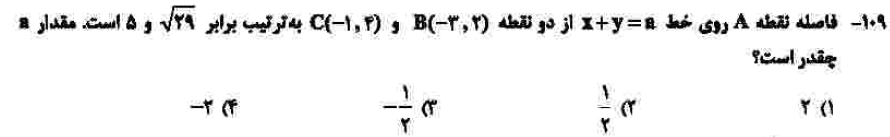
درجهی دشواری: د
مبحث: هندسه تحلیلی (فصل اول حسابان یازدهم)
کلید اولیهی سازمان سنجش: ۱
این سوال هم جز سوالات جدید است. رسیدن به ایدهی حل سوال اصلا کار سادهای نیست. برای حل ابتدا فاصلهی نقاط را از (x ,y) به دست میآوریم که اگر این دو معادله را از هم کم کنیم و به جای y آن a – x جایگذاری کنیم، a به دست میآید.

درجهی دشواری: الف
مبحث: ترکیب توابع (فصل دوم حسابان یازدهم)
کلید اولیهی سازمان سنجش: ۱
یک جایگذاری ساده است که باید سه بار تکرار شود. فقط برای رسیدن به پاسخ درست باید در محاسبات دقت کنید. هرچند روشهای دیگری نیز برای این سوال مانند روش تابع همانی وجود دارد.

درجهی دشواری: ج
مبحث: توابع نمایی و لگاریتمی (فصل سوم حسابان یازدهم)
کلید اولیهی سازمان سنجش: ۳
ابتدا هر دو فرض سوال را باید تبدیل به لگاریتم کنید و سعی کنید که تابع f را بر حسب x به دست آمده، بنویسید. اصلاً سوال سادهای نیست و نیاز به تسلط بالا بر قوانین لگاریتم بهویژه قانون تغییر مبنا دارد.
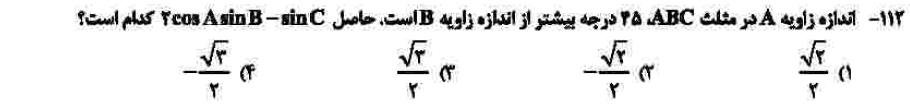
درجهی دشواری: ج
مبحث: مثلثات، روابط مربوط به تفاضل و جمع زوایا (فصل چهارم حسابان یازدهم)
کلید اولیهی سازمان سنجش: ۲
همانطور که میدانید مجموع سه زاویهی مثلث ۱۸۰ درجه است و اگر مجموع دو زاویه برابر با 180 باشد، sin برابر دارند، پس در خواستهی سوال، به جای sin C میتوان sin (A + B) نوشت و آن را با استفاده از فرمول باز کنید و با بقیهی خواستهی سوال جمع کنید در نهایت به sin (B – A) میرسید که طبق صورت سوال B – A دقیقاً منفی 45 درجه است. روش دیگر این است که زوایایی پیدا کنید که طبق صورت سوال درست باشند، مثلاً زوایای A، B و C را به ترتیب 90، 45 و 45 درجه در نظر بگیرید زیر یک دقیقه به پاسخ میرسید.
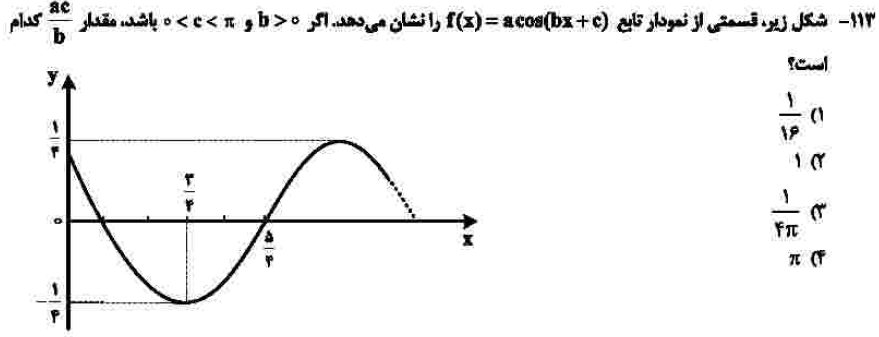
درجهی دشواری: ج
مبحث: نمودارهای مثلثاتی (فصل دوم حسابان دوازدهم)
کلید اولیهی سازمان سنجش: ۱
در ابتدا به سادگی مقدار a مثبت و منفی یک چهارم به دست میآید. سپس با توجه به نمودار و دوره تناوب، b و با توجه به جابجایی نمودار، c نیز به دست میآید. در نهایت با توجه به نمودار علامت a هم یافت میشود.
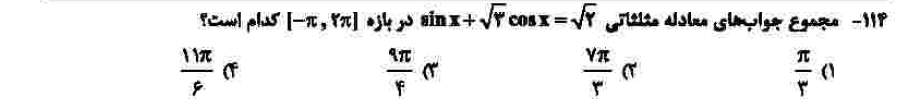
درجهی دشواری: ج
مبحث: معادلات مثلثاتی (فصل دوم حسابان دوازدهم)
کلید اولیهی سازمان سنجش: ۳
این سبک سوال بیشتر در نظام قدیم مطرح بود. البته در نظام جدید رشتهی ریاضی هم خارج از کتاب درسی محسوب نمیشود. برای حل، به جای رادیکال 3، tan 60 مینویسیم و همه را در cos 60 ضرب میکنیم. با این کار میتوانیم سمت چپ را به صورت sin جمع دو زاویه بنویسیم و سوال را حل کنیم.
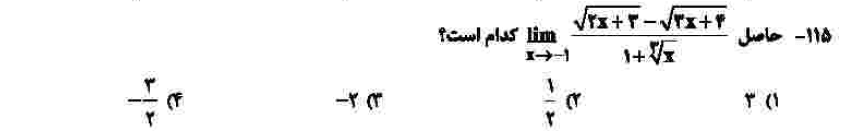
درجهی دشواری: ب
مبحث: حد و پیوستگی (فصل پنجم حسابان یازدهم)
کلید اولیهی سازمان سنجش: ۴
با جایگذاری منفی یک به حد مبهم صفر صفرم میرسیم که هوپیتال گیری سادهترین روش حل برای آن است. هرچند میتوانستید با ضرب صورت و مخرج در مزدوجهای صورت و مخرج، سوال را حل کنید.

درجهی دشواری: ب
مبحث: حد و پیوستگی (فصل پنجم حسابان یازدهم)
کلید اولیهی سازمان سنجش: ۳
اگر با دقت به بازههای داده شده نگاه کنید، در بازهی سوم اعداد بیشتر از یک مدنظر است که با توجه به جزصحیحهای داده شده، در بیشمار نقطهی صحیح ناپیوسته است. پس تابع نیز در بیشمار نقطه ناپیوسته است. بنابراین اصلاً نیازی به بررسی سایر ضابطهها نیست.

درجهی دشواری: ب
مبحث: تقسیم و بخشپذیری (فصل اول حسابان دوازدهم)
کلید اولیهی سازمان سنجش: ۴
وقتی از هر طبیعی حرف میزند بهتر است n را یک در نظر بگیرید. وقتی بر x + 2 بخشپذیر است، به ازای منفی دو حاصل صفر است که a با این روش پیدا میشود. از طرف دیگر ریشههای دومین مقسومعلیه یک و منفی سه است که به ازای یک، p برابر با 39 میشود و تنها در گزینهی چهار، به ازای یک به عدد 39 میرسیم.

درجهی دشواری: ج
مبحث: مجموع جملات دنبالههای حسابی و هندسی (فصل اول حسابان یازدهم)
کلید اولیهی سازمان سنجش: ۳
اگر دقت کنید جملات آخر دستههای دوم و بعد از آن تشکیل یک تصاعد هندسی با جملهی اول 3 و قدرنسبت 2 دادهاند. با همین اطلاعات، جملات آخر دستههای دوازدهم و سیزدهم را میبابیم. اگر به جملهی آخر دستهی دوازدهم یکی اضافه کنیم، جملهی اول دستهی سیزدهم به دست میآید. با توجه به متوالی بودن جملات، میانگین جملات دستهی سیزدهم، میانگین جملات اول و آخر آن است.

درجهی دشواری: ج
مبحث: مجانبها، حد در بینهایت و حد بینهایت (فصل سوم حسابان دوازدهم)
کلید اولیهی سازمان سنجش: 1
ابتدا حد تابع را در مثبت بینهایت و منفی بینهایت محاسبه میکنیم. ریشههای مخرج نیز به دست میآوریم. حال دو به دو این مقادیر را با هم برابر قرار میدهیم. در یکی از حالات b مثبت میشود که امکانپذیر نیست زیرا مخرج بدون ریشه میشود و مجانب قائمی نخواهیم داشت. بر همین اساس a و b به دست میآیند و با دقت به قدرمطلقها، حاصل حد خواسته شده را مییابیم.

درجهی دشواری: ب
مبحث: مشتق، خط مماس بر منحنی (فصل چهارم حسابان دوازدهم)
کلید اولیهی سازمان سنجش: ۲
ابتدا باید نقطهی تلاقی دو منحنی را بیابیم که برای به دست آوردن آن باید یک معادله مثلثاتی ساده را حل کنیم. با به دست آوردن آن، عرض را نیز با یکی از توابع به دست میآوریم. سپس معادلهی خط مماس در این نقطه را بر f مینویسم. با جایگذاری صفر در y، پاسخ به دست میآید.
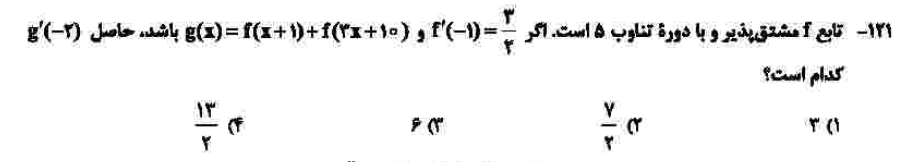
درجهی دشواری: ب
مبحث: ترکیب توابع متناوب و مشتق (فصل چهارم حسابان دوازدهم)
کلید اولیهی سازمان سنجش: ۳
ابتداز از تابع g مشتق میگیریم و با جایگذاری منفی 2، با توجه به متناوب بودن آن مقدار مشتق f در 4 هم برابر با سه دوم خواهد بود.
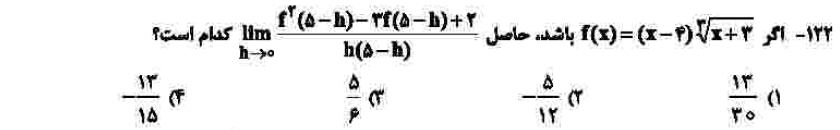
درجهی دشواری: ب
مبحث: تعریف مشتق (فصل چهارم حسابان دوازدهم)
کلید اولیهی سازمان سنجش: ۲
حل این سوال با استفاده از روش کتاب درسی، تقریباً امکان پذیر نیست. اما با جایگذاری صفر در حد، به صفر صفرم میرسیم و با هوپیتالگیری و اندکی محاسبات به پاسخ خواهید رسید.
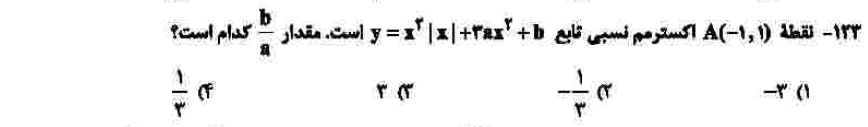
درجهی دشواری: الف
مبحث: کاربرد مشتق، اکسترمم نسبی (فصل پنجم حسابان دوازدهم)
کلید اولیهی سازمان سنجش: ۱
در این تابع، ابتدا خود A را جایگذاری میکنیم که یک معادله به ما میدهد. برای مشتقگیری ابتدا قدرمطلق را برمیداریم، و با برداشتن قدرمطلق، -x خارج میشود، زیرا مشتق را در منفی یک باید محاسبه کنیم. از طرف دیگر مقدار مشتق در منفی یک، صفر خواهد شد؛ زیرا اکسترمم نسبی تابع درجه سوم است. و این هم یک معادله دیگر به ما میدهد. با حل دو معادله دو مجهول موجود، مقادیر a و b به دست میآید.
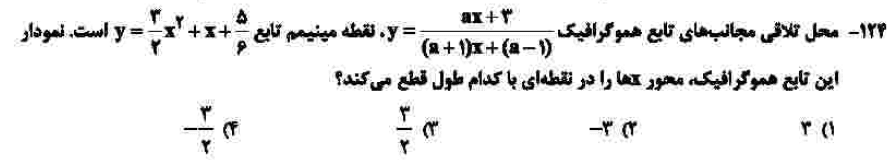
درجهی دشواری: ج
مبحث: ترکیب مجانبها و سهمی (فصل سوم حسابان دوازدهم و فصل چهارم ریاضی دهم)
کلید اولیهی سازمان سنجش: ۴
با حدگیری در بینهایت، مجانب افقی و یافتن ریشهی مخرج، مجانب قائم به دست میآید. نقطهی تلاقی این دو، دقیقاً راس سهمی است. در راس سهمی مشتق برابر صفر است که با جایگذاری مجانب قائم در مشتق سهمی، a به دست میآید. با جایگذاری a = 2 و y = 0 در معادلهی تابع هموگرافیک و حل معادله، پاسخ سوال نمایان میشود.
جمعبندی و کلام پایانی
قبل از هر چیز به جدول زیر که نشان دهندهی سطح ۲۱ سوال حسابان و ریاضی پایه این کنکور است، دقت کنید:
| سطح | ساده | متوسط | دشوار | بسیار دشوار |
| تعداد | ۲ | ۸ | ۹ | ۲ |
همانطور که دیدید ۲۱ سوال از ۵۰ سوال متعلق به حسابان و ریاضی پایه و ۲۴ سوال دیگر از هندسه و ریاضیات گسسته هستند. سازمان سنجش در کنکور داخل کشور رشتههای تجربی و انسانی سوالات بسیار سادهای ارائه داده بود اما این قاعده در رشتهی ریاضی رعایت نشده و سوالات هم جدید و هم دشوار بودند، البته میزان محاسبات سوالات برای رشتهی ریاضی منطقی بود. ایده پردازی مهمترین نقش در حل این سوالات را دارد.

